Wialon Hosting
Облачная версия Wialon, комплексное решение для цифровизации автопарка, разработанное для упрощения операций и повышения эффективности различных автопарков — от легковых и грузовых автомобилей до тяжелой техники и машин.
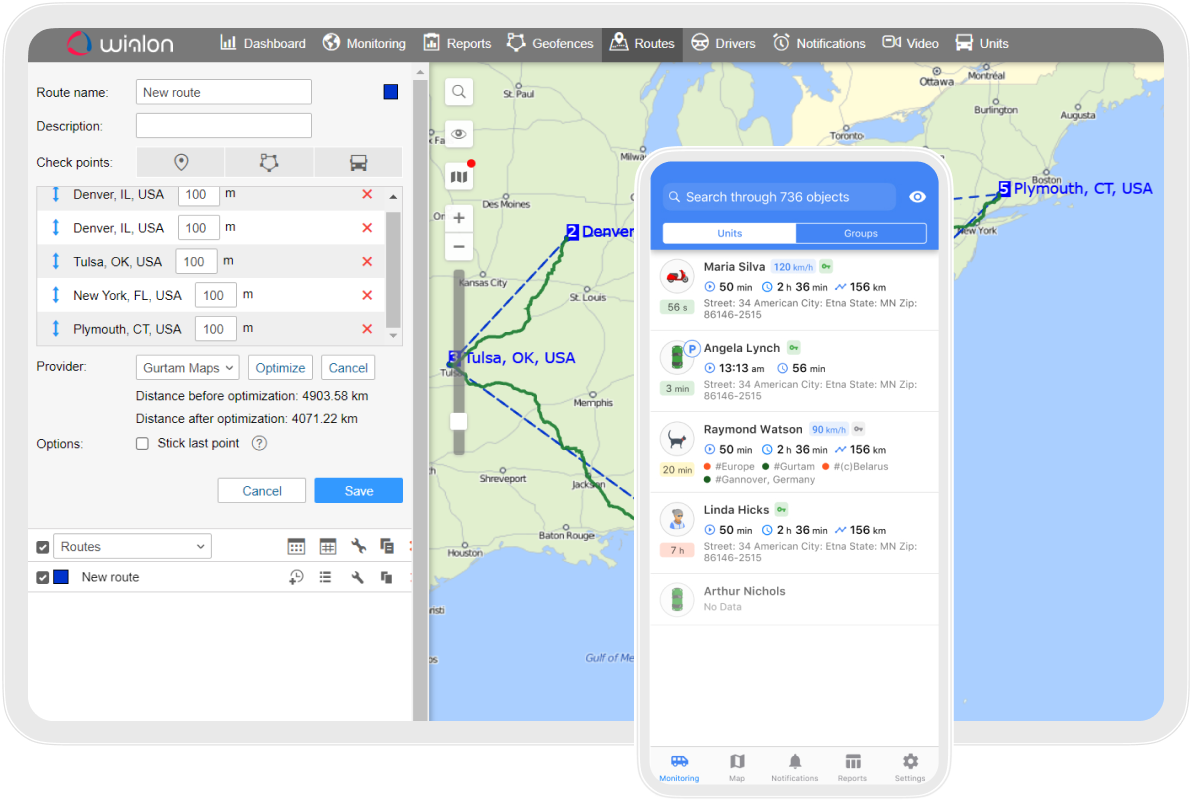
Облачная версия Wialon, комплексное решение для цифровизации автопарка, разработанное для упрощения операций и повышения эффективности различных автопарков — от легковых и грузовых автомобилей до тяжелой техники и машин.
